Kmeans est l’algorithme de clustering le plus utilisé en Data Science pour une raison simple : il offre le meilleur compromis entre rapidité d’exécution et facilité d’interprétation. Plutôt que de prédire une valeur, il structure l’information en détectant des motifs naturels dans vos données.
Qu’est-ce que le kmeans ?
Le kmeans est un algorithme d’apprentissage non supervisé. Contrairement aux méthodes supervisées qui s’appuient sur des données étiquetées (ex: prédire un prix), la méthode kmeans travaille « à l’aveugle » sur des données brutes.
Son but est de partitionner un jeu de données en un certains nombre de groupes distincts (clusters). La valeur k correspond au nombre de groupes. L’algorithme cherche à résoudre simultanément deux contraintes géométriques :
- Cohésion : Les points d’un même groupe doivent être très proches les uns des autres (minimiser la distance au centre du groupe).
- Séparation : On cherche à maximiser la distance entre les groupes pour qu’ils soient le plus séparés possible.
Comment fonctionne kmeans ?
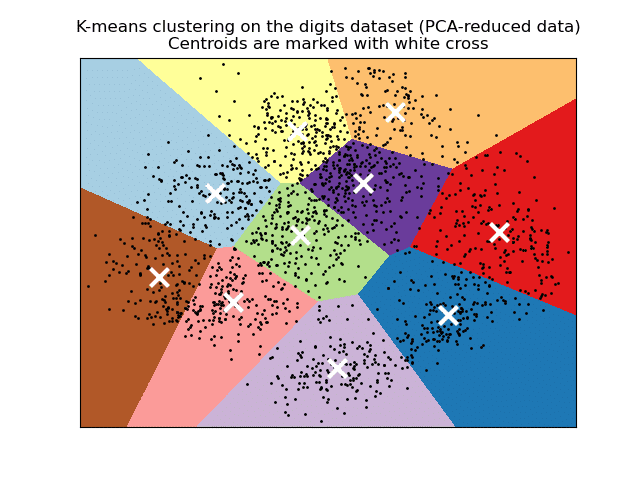
La mécanique du K-Means est itérative. Il repose sur la notion de centroïde, un point fictif qui représente le centre de gravité d’un cluster.
Le cycle se déroule en quatre étapes :
- Initialisation : On définit le nombre de clusters k. L’algorithme place aléatoirement k centroïdes dans l’espace des données.
- Affectation (assignment) : Chaque point de données est assigné au centroïde le plus proche (selon la distance euclidienne).
- Mise à jour (update) : On recalcule la position des centroïdes. Le nouveau centroïde devient la moyenne exacte des positions de tous les points qui lui ont été assignés.
- Convergence : On répète les étapes 2 et 3. L’algorithme s’arrête quand les centroïdes se stabilisent ou qu’un nombre maximal d’itérations est atteint.
Petite précision sur l’initialisation de kmeans. Une initialisation purement aléatoire peut piéger l’algorithme dans une configuration sous-optimale.
La variante kmeans++ (activée par défaut dans Scikit-learn) place les premiers centroïdes de manière intelligente (éloignés les uns des autres), ce qui accélère la convergence et améliore la qualité finale du clustering.
L’importance de la normalisation des données
La méthode kmeans calcule des distances euclidiennes. Il est donc extrêmement sensible aux échelles de grandeur.
Voici un exemple d’erreur classique. Si vous croisez une variable « Âge » (0 à 100) avec une variable « Salaire » (20 000 à 100 000), la dimension « Salaire » aura un poids 1000 fois supérieur dans le calcul de distance et l’âge deviendra négligeable.
La solution : il faut systématiquement standardiser les données (via StandardScaler ou MinMaxScaler) pour que toutes les variables aient le même poids (moyenne à 0 et écart-type à 1).
Comment choisir la bonne valeur de k dans kmeans ?
L’algorithme ne détermine pas le nombre de groupes idéal seul, c’est un hyperparamètre que vous devez définir. Voici deux méthodes pour l’estimer objectivement :
La méthode du coude (Elbow Method)
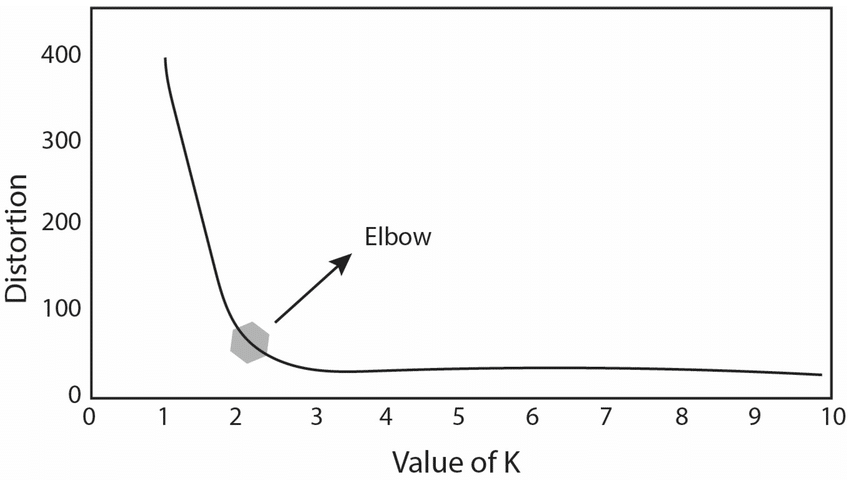
On entraîne le modèle sur une plage de k (ex: de 1 à 10) et on observe la baisse de l’inertie (la somme des distances au carré).
L’inertie baisse mécaniquement quand k augmente. Il faut repérer le point d’inflexion (« le coude ») où le gain de performance devient marginal par rapport à la complexité ajoutée d’un cluster supplémentaire.
Le coefficient de silhouette
C’est une métrique de validation plus fine qui varie entre -1 et 1. Elle mesure si un point est bien « chez lui » (proche de ses voisins de cluster) par rapport au cluster voisin le plus proche.
Plus le score est proche de 1, plus les clusters sont denses et bien séparés.

Quelles sont les applications de la méthode kmeans ?
Au-delà de la théorie, kmeans trouve de nombreuses applications concrètes.
En marketing, il est notamment utilisé pour la segmentation RFM afin de regrouper les clients selon leur récence d’achat, leur fréquence et le montant dépensé.
En traitement d’images, il permet de quantifier une image en réduisant le nombre de couleurs possibles pour la compresser tout en conservant ses caractéristiques essentielles.
Enfin, il peut servir à la détection d’anomalies, en identifiant les points très éloignés des centroïdes après convergence, typiquement des comportements suspects, des fraudes ou des signaux de défauts machine.
Implémentation de kmeans avec Python
Voici une structure de code en Python avec scikit-learn pour lancer un kmeans :
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
# --- 1. Chargement des données (Cas réel) ---
# Le dataset Iris contient 150 échantillons de 3 espèces de fleurs différentes.
iris = load_iris()
X = iris.data # Les mesures (features)
# Pour la lisibilité, on le met dans un DataFrame (optionnel mais recommandé)
df = pd.DataFrame(X, columns=iris.feature_names)
print("Aperçu des données brutes :")
print(df.head())
# --- 2. Préparation (Mise à l'échelle) ---
# Comme vu dans l'article, on normalise pour que les "cm" aient tous le même poids
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# --- 3. Configuration & Entraînement ---
# On choisit k=3 car on sait qu'il existe 3 espèces dans ce dataset.
# Dans la vraie vie (sans savoir), on aurait utilisé la méthode du coude.
kmeans = KMeans(n_clusters=3, init='k-means++', random_state=42)
kmeans.fit(X_scaled)
# --- 4. Exploitation des résultats ---
# On récupère les labels (0, 1 ou 2) attribués par l'algo
clusters = kmeans.labels_
# On ajoute le cluster au DataFrame pour analyse
df['cluster_kmeans'] = clusters
# --- 5. Visualisation (La preuve par l'image) ---
# On visualise 2 dimensions : Longueur du pétale vs Largeur du pétale
plt.figure(figsize=(10, 6))
# Affichage des points, colorés selon leur cluster K-Means
plt.scatter(X_scaled[:, 2], X_scaled[:, 3], c=clusters, cmap='viridis', s=50, alpha=0.8, label='Fleurs')
# Affichage des Centroïdes (les croix rouges)
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 2], centers[:, 3], c='red', s=200, marker='X', label='Centroïdes')
plt.title('Résultat du K-Means sur le dataset Iris')
plt.xlabel('Longueur du pétale (normalisée)')
plt.ylabel('Largeur du pétale (normalisée)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()
# Comparaison rapide (optionnelle)
print("\nRépartition des fleurs par cluster trouvé :")
print(df['cluster_kmeans'].value_counts())Conclusion
Le K-Means est l’algorithme exploratoire par excellence. Il est imparfait sur des géométries complexes (où des algorithmes basés sur la densité comme DBSCAN sont supérieurs), mais sa rapidité en fait le premier test à effectuer pour comprendre la structure d’un jeu de données inconnu.


Laisser un commentaire