Qu’est ce qu’un réseau LSTM ?

L’un des avantages majeurs des réseaux de neurones réside dans la diversité de leurs architectures. Si les Transformers dominent aujourd’hui l’actualité, comprendre les LSTM (Long Short-Term Memory) est indispensable pour saisir comment les machines traitent les données séquentielles (texte, séries temporelles, audio).

Dans cet article, nous plongeons au cœur de cette architecture ingénieuse conçue pour résoudre l’un des plus grands défis du Deep Learning : la mémoire.

Des réseaux de neurones récurrents (RNN) aux LSTM

Pour comprendre les LSTM, il faut d’abord regarder leurs prédécesseurs : les réseaux de neurones récurrents (RNN).

Contrairement aux réseaux classiques qui traitent chaque donnée isolément, les RNN possèdent une mémoire à court terme. Ils traitent les informations en séquence, conservant une trace de ce qui vient de se passer. C’est idéal pour comprendre une phrase, car le sens d’un mot dépend souvent des précédents.

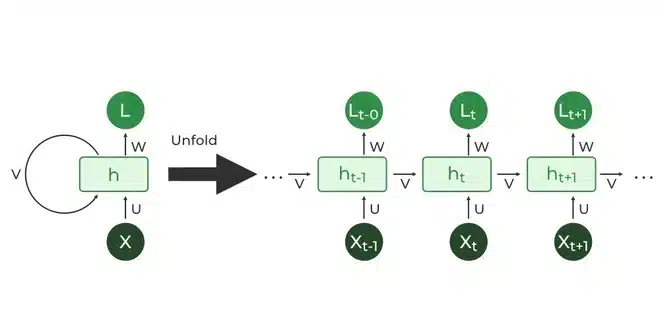
Illustration d'un réseau RNN (Geeksforgeek)
Illustration d’un réseau RNN (Geeksforgeek)

Les limites de RNN

Les RNN sont théoriquement capables de relier des informations distantes. En pratique, c’est une autre histoire.

Lors de l’entraînement, le réseau utilise la rétropropagation pour ajuster ses poids en « remontant le temps ». Le problème survient quand la séquence est longue : les gradients (les signaux d’erreur) doivent traverser de nombreuses étapes de multiplication successives.

Cela peut créer deux effets indésirables majeurs :

  1. Vanishing Gradient (Disparition) : Si les nombres sont petits (< 1), à force d’être multipliés, le gradient tend vers 0. Le réseau « oublie » alors le début de la phrase, rendant l’apprentissage du contexte impossible.
  2. Exploding Gradient (Explosion) : Si les nombres sont grands, le gradient devient infini et le réseau diverge complètement.
Illustration du vanishing et exploding gradient
Illustration du vanishing et exploding gradient (Substack)

Quelle est la solution pour éviter le problème de vanishing gradient ?

Une solution célèbre à ce problème est l’utilisation de Skip Connections (ou connexions résiduelles), popularisée par les réseaux ResNet en computer vision.

L’idée est de créer des « raccourcis » qui permettent au gradient de sauter certaines couches pour ne pas disparaître. Comme si on transmettait un rappel de l’information, en partant des premières couches du réseau en direction des dernières couches.

D’ailleurs, les architectures modernes utilisées pour entraîner les LLM, comme les Transformers (GPT, BERT), utilisent massivement ces connexions résiduelles pour entraîner des réseaux très profonds.

Cependant, pour les architectures récurrentes pures, la géométrie est différente : le problème n’est pas tant la profondeur du réseau que la longueur de la séquence. La solution qui nous intéresse donc aujourd’hui se nomme LSTM.

Long Short-Term Memory

Comme nous l’avons vu, les RNN peinent à retenir l’information sur la durée. Les LSTM (Long Short-Term Memory) ont été conçus spécifiquement pour résoudre ce problème.

Leur nom est un oxymore apparent : une « mémoire à long terme… à court terme ». En réalité, cela signifie qu’ils possèdent une mémoire de travail (court terme) capable de persister suffisamment longtemps pour relier des informations distantes.

Comparaison entre les RNN et les LSTM
Comparaison entre les RNN et les LSTM

L’idée principale derrière les LSTM : le cell state

La principale innovation des LSTM est de diviser le signal qui traverse le réseau en deux flux distincts :

  1. Le Hidden State (h_t) : C’est la mémoire à court terme. Elle correspond à la sortie immédiate du réseau à un instant t (similaire aux RNN classiques).
  2. Le Cell State (C_t) : C’est la mémoire à long terme.

Imaginez le Cell State comme un tapis roulant qui file tout droit le long de la chaîne de séquence. L’information peut y circuler presque sans interruption. C’est grâce à cette « autoroute » que le gradient peut remonter loin dans le passé sans disparaître.

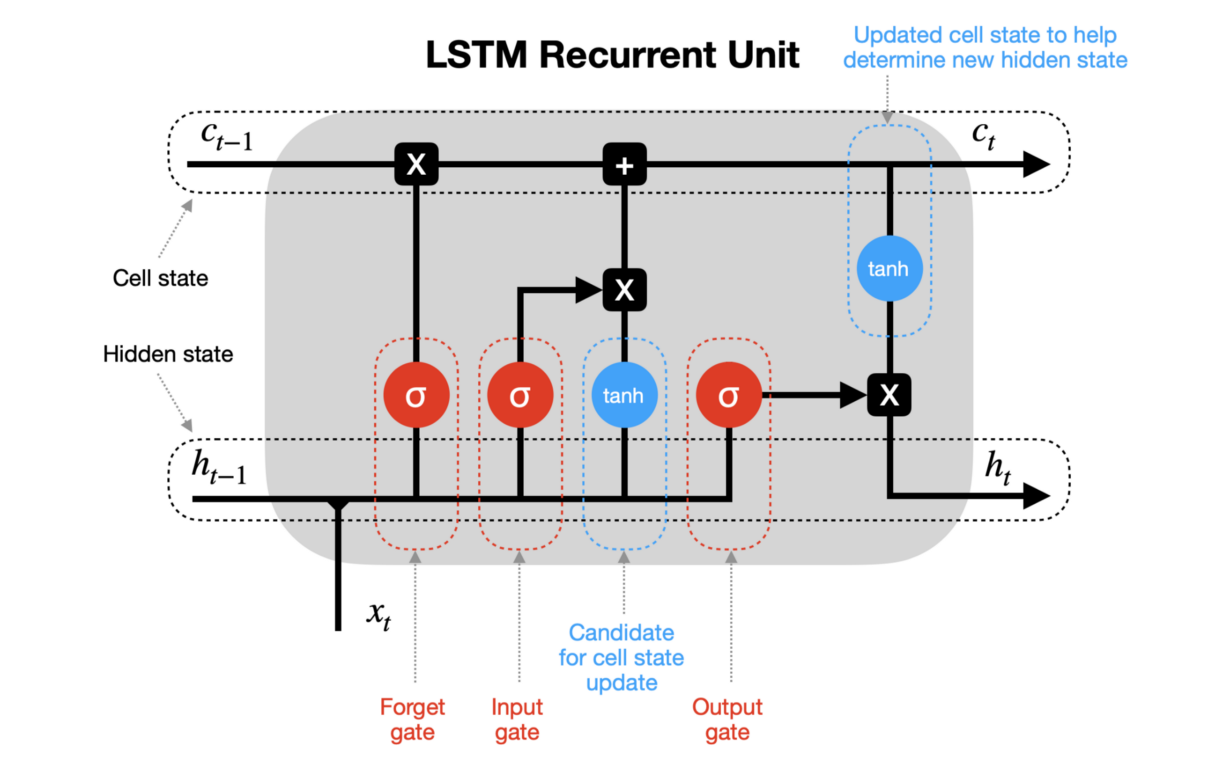
Architecture d’une cellule de LSTM : les 3 portes

Pour contrôler ce tapis roulant (ajouter ou retirer des valises d’information), la cellule LSTM utilise des mécanismes appelés gates (portes).

Une cellule effectue un cycle précis en 3 étapes majeures :

1 – Forget Gate

La première étape est une décision de nettoyage. Le réseau regarde l’état précédent h_{t-1} et la nouvelle entrée x_t pour décider ce qu’il faut oublier du Cell State.

  • Exemple : Si on analyse un texte et qu’on rencontre un point « . ». C’est le moment d’oublier le sujet de la phrase précédente.

Cela se fait via une fonction sigmoïde (sigma) qui sort un nombre entre 0 (tout oublier) et 1 (tout garder).

ft=σ(Wf⋅[ht−1,xt]+bf)f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)

2 – Input Gate

Ensuite, on décide quelles nouvelles informations méritent d’être stockées sur le tapis roulant (le Cell State).

  • Une sigmoïde décide quelles valeurs mettre à jour (i_t).
  • Une fonction tanh crée un vecteur de nouvelles valeurs candidates :
C~t\tilde{C}_t

Ces deux parties sont combinées pour mettre à jour l’état de la cellule : l’ancien état est multiplié par le facteur d’oubli, et on y ajoute les nouvelles informations importantes.

Ct=ft⋅Ct−1+it⋅C~tC_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t
schèma d'un neurone lstm
Schéma simplifié d’une cellule d’un réseau LSTM

3 – Output Gate

Enfin, le réseau doit générer son Hidden State (h_t) pour l’instant présent. Il ne va pas « cracher » tout le contenu de sa mémoire long terme. Il va le filtrer.

On décide quelle partie du Cell State on veut exposer en sortie, et on lui applique une non-linéarité (tanh).

ot=σ(Wo⋅[ht−1,xt]+bo)o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)
ht=ot⋅tanh⁡(Ct)h_t = o_t \cdot \tanh(C_t)

La relation de récurrence d’un LSTM est donc bien plus complexe que celle d’un RNN classique. Elle prend en entrée trois éléments pour produire deux sorties :

ht,Ct=LSTM(xt,ht−1,Ct−1)h_t, C_t = \text{LSTM}(x_t, h_{t-1}, C_{t-1})

C’est cette mécanique de précision qui permet aux LSTM de « choisir » de se souvenir qu’un sujet était au pluriel au début d’un paragraphe pour accorder un verbe dix lignes plus loin.

Cellule d'un réseau LSTM
Cellule d’un réseau LSTM (Research gate)

Limites de l’architecture LSTM

Malgré le fait que les LSTM règlent en grande partie le problème de disparition du gradient (Vanishing Gradient), cette architecture n’est pas une « balle en argent ». Elle présente des défauts structurels qui ont motivé la recherche vers des modèles plus récents comme les Transformers.

La complexité et le risque d’Overfitting

Un réseau LSTM est beaucoup plus complexe qu’un RNN standard. Pour chaque cellule, au lieu d’une seule opération, le réseau doit apprendre les poids de quatre composants distincts (les trois portes + le candidat au cell state).

Cette multiplication des paramètres rend le modèle très puissant, mais aussi très enclin à l’Overfitting (surapprentissage).

  • Le problème : Le modèle finit par « apprendre par cœur » le bruit des données d’entraînement au lieu de comprendre la logique générale. Il devient alors incapable de généraliser sur de nouvelles données.
  • La solution partielle : On utilise souvent des techniques de régularisation comme le Dropout (désactiver aléatoirement certains neurones pendant l’entraînement) pour forcer le réseau à être plus robuste.
Schémas de l’overfitting et underfitting

Lenteur et absence de parallélisation

C’est sans doute le défaut qui a coûté aux LSTM leur place de leader en NLP.

De par leur nature récurrente, les LSTM sont séquentiels. Pour calculer l’état à l’étape t, vous êtes obligé d’attendre le résultat de l’étape t – 1.

  • Impossible d’utiliser toute la puissance des GPU modernes qui excellent dans le calcul parallèle.
  • L’entraînement sur de très longs textes est donc extrêmement lent comparé aux architectures modernes (Transformers) qui peuvent traiter toute une phrase d’un seul coup.

Sensibilité à l’initialisation (instabilité)

Comme mentionné précédemment, les réseaux de neurones sont sensibles à la manière dont on initialise leurs poids au tout début de l’entraînement.

Le LSTM ne fait pas exception : une initialisation aléatoire « malchanceuse » peut conduire le modèle à rester coincé dans un optimum local (une solution médiocre dont il n’arrive pas à sortir).

Le modèle peut parfois converger très vite, et d’autres fois ne rien apprendre du tout avec les mêmes données, simplement à cause de ces valeurs de départ.

Une mémoire « Long Terme »… mais limitée

Enfin, bien que le LSTM soit bien meilleur que le RNN, sa mémoire n’est pas infinie. Sur des séquences très longues (par exemple un texte de plusieurs milliers de mots), le Cell State finit tout de même par être saturé ou bruité, et le réseau perd le fil du contexte initial.

C’est là que les mécanismes d’attention, qui permettent de regarder n’importe quel endroit du passé sans limite de distance, ont pris le relais.

Implémentation des LSTM avec Python

Maintenant qu’on a vu le côté théorique derrière les réseaux LSTM, il est temps de voir le côté pratique et comment ils peuvent être utilisés pour faire des choses assez originales et drôles.

Après avoir récolté les paroles de plus de 100 rappeurs français sur Genius en utilisant à la fois l’API et des techniques de Web Scraping avec BeautifulSoup, j’ai entraîné un petit réseau LSTM à générer des paroles de rap français à partir d’une petite phrase en input.

Vous pouvez retrouver tout le code et le dataset utilisé sur le repo git suivant : https://github.com/Adib-Habbou/french-rap-lyrics-generator

Le modèle s’avère être assez vulgaire et grossier, ce qui nous rappelle encore une fois qu’un modèle c’est avant tout les données sur lesquelles on l’entraîne et que si l’on ne fait pas attention aux données qu’on lui donne, on peut malheureusement se retrouver avec des résultats inattendues voire dangereux.

Comme cela s’est avéré être le cas pour l’IA de Microsoft Tay qui est très vite devenue raciste à cause des tweets sur lesquelles le modèle a été entraîné, ou encore les modèles DALL-E d’OpenAI qui comportent un bon nombre de biais racistes et misogynes.