Optimisation de fonctions, descentes de gradient : applications aux réseaux de neurones

En mathématiques l’optimisation est une discipline qui cherche à résoudre des problèmes de minimisation de fonctions. Les applications sont diverses : recherche du chemin le plus court, optimisation des processus industriels, choix des meilleurs investissements financiers, etc.

L’optimisation est un des domaines des maths qui intervient le plus en machine learning, et s’il est important(tissime !), ce n’est pas pour rien ! Nous verrons, que les algorithmes d’optimisation sont des outils centraux pour l’entraînement de modèles par réseaux de neurones.

Optimisation pour les problèmes de régressions

Laisser moi d’abord définir ce qu’est une régression. Les méthodes de régressions sont des techniques qui permettent de comprendre et de quantifier la relation qu’il peut y avoir entre deux variables. Une fois que vous avez un modèle vous pourrez alors faire des prédictions.

Les choses seront plus claires avec cet exemple. On souhaite prédire le loyer d’un appartement en fonction de sa surface (pour Paris ça ne marche pas !).
On a un certain nombre de données qui nous permettent de construire ce nuage de points :

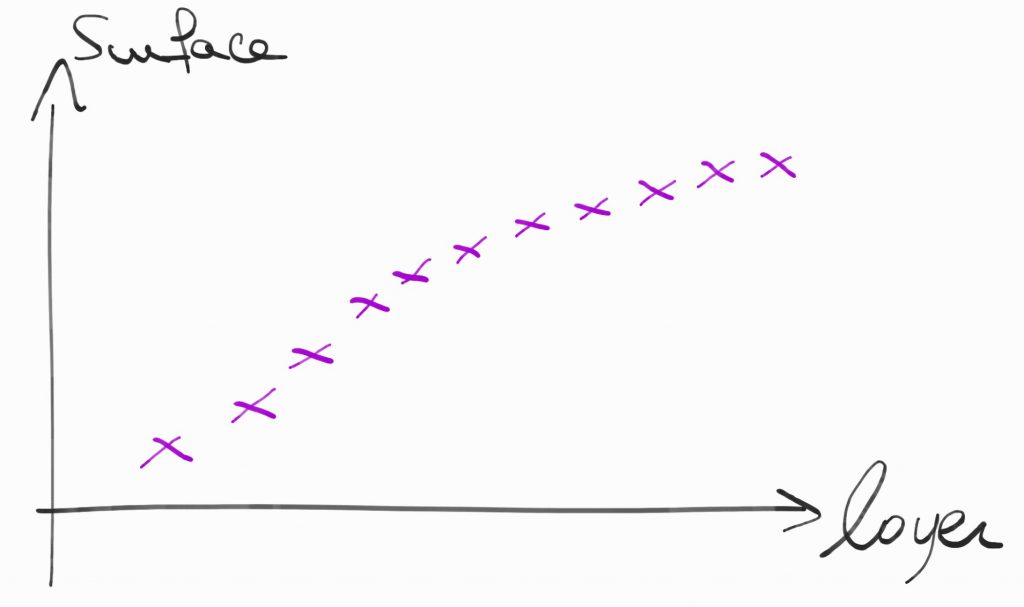
On voit bien que les données semblent suivre une certaine tendance. La régression c’est simplement trouver la courbe qui collera le mieux aux nuages de points.

On pourrait avoir cette courbe-là par exemple :

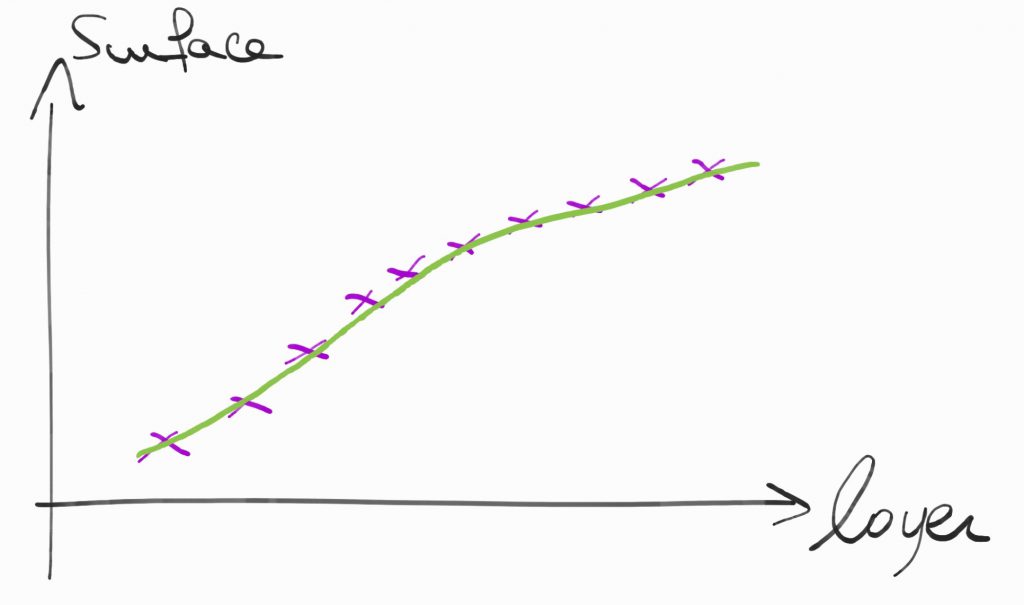
Maintenant que notre modèle est construit, on peut faire des prédictions, on peut estimer le loyer en fonction de la surface d’un appartement.

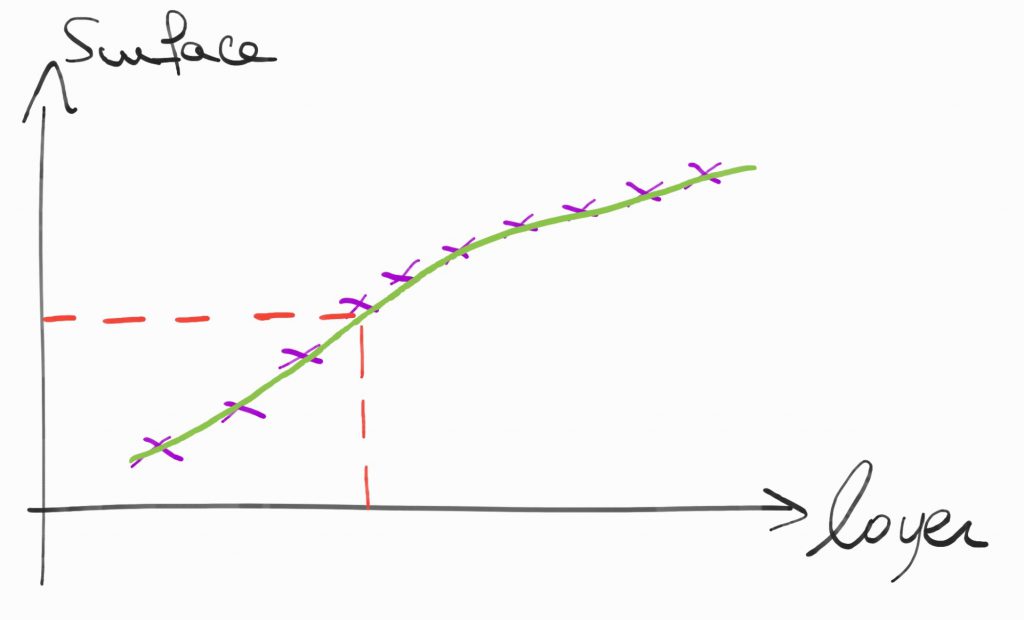
Pour ce type de problèmes, l’optimisation numérique permet de trouver la courbe qui va fiter le mieux les données. On cherchera souvent la courbe qui minimise la somme des carrés des erreurs. On prend le carré pour des raisons de régularité (l’optimisation est souvent une question de gradients et de Hessienne on veut des fonctions différentiables).

Evidemment cet exemple est très simplifié. Le loyer d’un appartement dépend en réalité d’un certain nombre d’autres paramètres. Néanmoins le principe est le même, l’optimisation se fera en dimension plus grande pour les variables quantitatives. Par contre, si vous incluez des variables qualitatives comme est-ce que l’appartement est meublé ou non, la conception du modèle devient un peu moins évidente.

Réseaux de neurones

Pour la construction et l’entraînement de réseaux de neurones, l’optimisation est très présente. De manière schématique, un réseau de neurone peut être vu comme une immense machine avec des boutons que l’on peut tourner pour paramétrer notre réseau. On veut donc trouver un ensemble de positions des boutons (de réels) qui permet de minimiser la fonction de coût (notre fonction d’erreur).

En pratique, nos données sont partagées en deux, les données d’entrainements et les données de test. Le réseau de neurones est une machine qui à partir d’une donnée d’entrée, construit une sortie. On va donc entrainer notre réseaux jusqu’à ce que les sorties pour nos données d’entrainements soient aussi proches que possible de ce que l’on veut. Pour cela il faut minimiser l’erreur entre la sortie de notre réseau et la sortie souhaitée. C’est là que l’optimisation intervient ! La plupart du temps ceux sont les méthodes de descentes de gradient qui sont utilisées pour minimiser cette erreur, ça tombe bien je vous explique ces méthodes en partie 3 !

Une des problématiques classiques que l’on rencontre en machine learning est le choix de la topologie du réseau de neurones. On souhaite trouver les hyper-paramètres (nombres de couches, nombres de neurones, dispositions, etc.) qui permettent d’avoir un résultat optimal. Les méthodes d’optimisations utilisées pour ça sont : grid search, random search ou encore SMBO (Sequential Model-Based Optimisation : c’est une approche bayésienne très jolie, si vous connaissez un peu les stat cette méthode vous plaira !).

Méthodes de descentes de gradients

Pour toutes les méthodes de descentes de gradient le principe est le même, on cherche à s’approcher étape après étape du minimum d’une fonction (dont l’expression est souvent inconnue). Pour se faire, on choisit un point initial et on évalue la valeur de la dérivée de la fonction en ce point (on a souvent uniquement une approximation). Selon le signe de la dérivée, on se déplace vers la droite ou vers la gauche jusqu’à être assez proche du minimum.

Pour l’itération on fixe un pas que l’on appelle learning rate. C’est ce pas qui détermine à quel point on se décale de la position initiale.Cette méthode peut sembler un peu compliquée à appréhender pour les plus allergiques aux maths d’entres vous, mais elle est finalement assez intuitive. Elle est très facile à visualiser sur un schéma pour une fonction à une dimension :

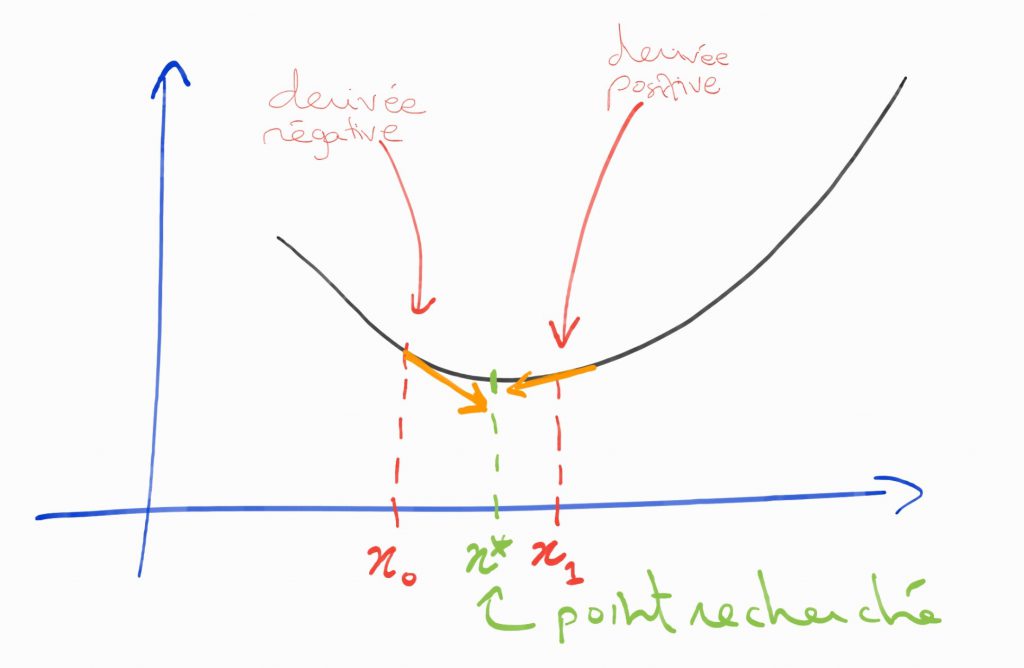
A chaque point où l’on se trouve, on calcul la dérivée de la fonction en ce point. Si la dérivée est négative cela signifie que la fonction est décroissante au voisinage de ce point et que l’on doit se déplacer vers la droite. Au contraire une dérivée positive, signifie que l’on doit se déplacer vers la gauche. On réitère ce processus jusqu’à ce que l’on atteigne un nombre d’itérations maximum ou que l’on estime être assez proche du minimum.
L’algorithme est en fait très simple :

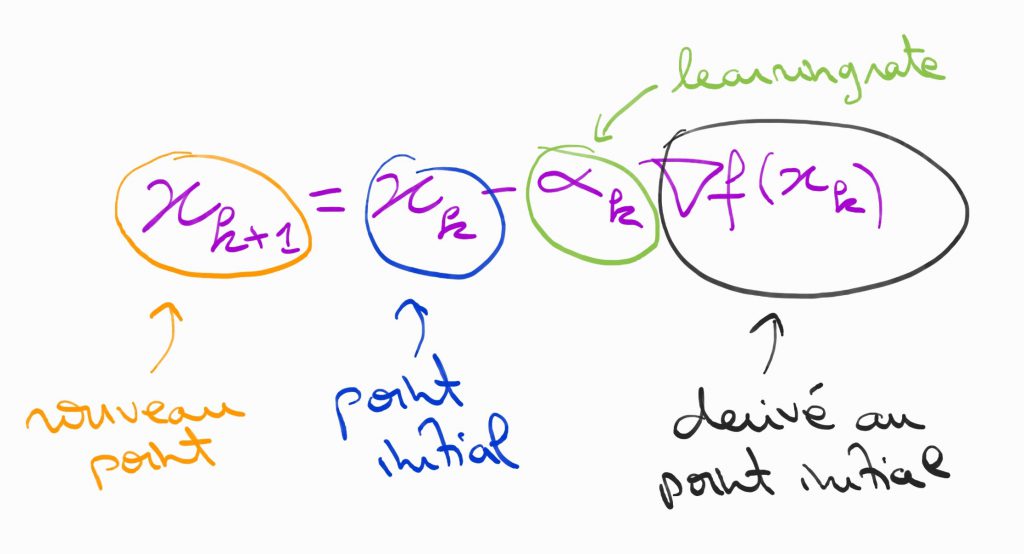
Attention, le choix du learning rate doit être fait de façon intelligente ! Un learning rate trop grand ne permettra pas de s’approcher assez du minimum, un learning rate trop petit peut augmenter de façon significative le temps de calcul et n’oubliez pas qu’en deep learning on veut optimiser des fonctions de dimensions très élevées (qui peuvent parfois dépasser le million).

Pour ce faire, il existe un certain nombre de méthodes de gradients avec des learning rate qui dépendent de la fonction à optimiser : gradient à pas optimal, BFGS (Broydem, Fletcher, Goldfard, Shanno), Barzilaï-Borwein (toujours pas démontrée, vous pouvez essayer si vous avez le temps !), etc.

Ça c’était pour la bonne nouvelle. Malheureusement, comme nous ne sommes pas dans le monde des bisounours (dommage !), ces méthodes ont leurs limitations. D’abord, les méthodes de descentes de gradient imposent des conditions de régularités assez strictes sur les fonctions à optimiser. Elles doivent être convexe et différentiable. Deuxièmement, on trouve un minimum local seulement (sur un intervalle fixé), rien ne nous garantit qu’un point plus bas n’existe pas à un autre endroit… Enfin, ce sont des méthodes qui peuvent parfois être coûteuses en temps, surtout lorsque le calcul du learning rate nécessite de calculer des dérivées secondes.

J’avoue que je suis un peu dur avec les algorithmes de descentes de gradients… Ces méthodes ne sont pas parfaites mais elles fonctionnent très bien en machine learning et pour beaucoup d’autres applications. Et en plus on n’a pas vraiment d’alternatives 😅