Ilyes TALBI | Samir JEETO | Valentin DORE
Mon attrait pour le machine learning vient du fait qu’il n’a quasiment aucune limites en termes d’applications. Dès que vous avez des données, vous pourrez faire des choses intéressantes avec. Et ceux quelque soit la nature de vos données.
Images, vidéos, textes, sons, laissez vous guider par votre imagination !
Dans cet article, que je vous ai préparé avec 2 amis, on vous explique comment entraîner des modèles de classification automatique de musiques. Nous passerons pas mal de temps sur le nettoyage et la préparation des données d’entraînement. Nous entraînerons ensuite plusieurs modèles de classifications afin de pouvoir les comparer.
Données et préparation de l’environnement de travail
Pour ce projet nous utiliserons la base GTZAN. Elle comporte 1000 pistes de 30 secondes chacune, réparties suivant 10 classes différentes :
- Blues
- Classic
- Country
- Disco
- Hip-Hop
- Jazz
- Métal
- Pop
- Reggae
- Rock
Le fichier fait 1.2Gb mais vous pouvez télécharger une version plus petite avec 600 pistes (60 par genre).
Pour le traitement des données sonores on utilise souvent la librairie Librosa sur Python, c’est ce que l’on va utiliser pour ce projet.
Comme d’habitude nous travaillerons sur Google Colab, nous aurons besoin de paralléliser certains calculs sur GPU pour qu’ils soient effectués plus rapidement (pour l’optimisation des hyperparamètres et entraînement d’un CNN).
J’ai mis tous les codes à disposition sur colab.
Commençons par importer toutes les librairies qui vont nous servir :
import pandas as pd # Pour le dataframe
import numpy as np # Pour la normalisation et calculs de moyenne
import matplotlib.pyplot as plt # Pour la visualisation
from PIL import Image
import librosa # Pour l'extraction des features et la lecture des fichiers wav
import librosa.display # Pour récupérer les spectrogrammes des audio
import librosa.feature
import os # C'est ce qui va nous permettre d'itérer sur les fichiers de l'environnement de travail
from sklearn.feature_selection import VarianceThreshold
from sklearn.model_selection import train_test_split, GridSearchCV, validation_curve, RandomizedSearchCV # Split de dataset et optimisation des hyperparamètres
from sklearn.ensemble import RandomForestClassifier # Random forest
from sklearn.ensemble import GradientBoostingClassifier # XGBoost
from sklearn.neighbors import KNeighborsClassifier # k-NN
from sklearn.svm import SVC # SVM
from sklearn.metrics import accuracy_score, confusion_matrix, recall_score, f1_score, zero_one_loss, classification_report # Métriques pour la mesure de performances
from sklearn.preprocessing import normalize, StandardScaler
import tensorflow as tf # Pour le reseau de neurones simple et pour le CNN
import seaborn as sns
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.optimizers import Adam
from keras.utils import to_categorical
from xgboost import XGBClassifier
from pprint import pprintExtraction des features
La première étape de notre projet est l’extraction de features. On cherche des données à tirer de nos pistes audio qui contiennent assez d’informations pour pouvoir séparer les musiques le mieux possible.
Cette étape, qui est primordiale quelque soit le projet de machine learning sur lequel vous travaillez, dépend beaucoup de l’application. Elle nécessite une bonne connaissance des données que vous souhaitez exploiter.
Dans notre cas on peut retenir 23 features qui permettront d’obtenir de bons résultats :
- Zero Crossing Rate
- Spectral centroid
- Spectral Roll-Off Point
- Mel-Frequency Cepstral (20 coefficients)
Détaillons un peu ce que ces features représentent.
ZCR : Zero Crossing Rate
Le ZCR est un indicateur proportionnel au taux de changement de signe d’un signal musical. Il est très utilisé pour la reconnaissance vocale et semble être un critère intéressant pour faire de la classification de musiques.
De façon général cette métrique est très utilisées dès qu’on a un signal avec une évolution temporelle. Dans notre cas on prend 0 comme valeur, mais peut adapter la métrique à des signaux positives par translation.
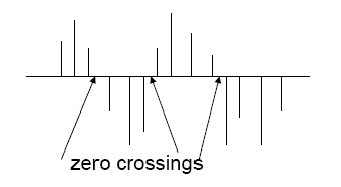
Sa valeur est donnée par l’expression suivante :
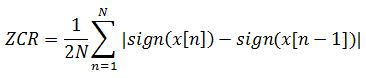
On peut calculer cette métrique facilement avec Librosa :
audio = librosa.load('votre_musique.wav')[0]
zcr = librosa.zero_crossings(audio)audio représente le np.array du fichier audio.
Spectral centroid
Le spectral centroid est une métrique utilisée pour caractériser les spectres des musiques. Il s’agit d’un indicateur géométrique de la position du centre de masse du spectre d’un son.
Dans l’étude des timbres musicaux on parle parfois de brightness, beaucoup considèrent cette caractéristique comme étant l’un des facteurs les plus discriminants entre des musiques. C’est un indicateur de la quantité de fréquences hautes qui composent le son. Et le spectral centroid constitue un moyen fiable pour mesurer cette caractéristique.
Sa formule est simplement la moyenne pondérée des signaux par des coefficients x(i) :
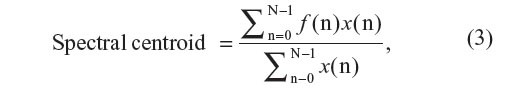
MFCC : Mel-Frequency Cepstral Coefficients
Les MFCC sont des coefficients cepstraux qui correspondent à une transformation sinusoïdale de la puissance d’un signal. Le calcul de ces coefficients se fait suivant ces différentes étapes :
- Calcul de la transformée de Fourier de la trame à analyser
- Pondération du spectre d’amplitude (ou de puissance selon les cas) par un banc de filtres triangulaires espacés selon l’échelle de Mel
- Calcul de la transformée en cosinus discrète du log-mel-spectre
Source : Wikipédia
Spectral Roll-Off Point
Cette feature est une mesure de l’asymétrie à droite d’un spectre sonore. Elle est utilisée par exemple pour différencier des paroles chantées et des paroles normales (cf Scheirer & Slaney).
Construction du pipeline et du dataframe
Maintenant que nous avons présentés ces métriques, nous pouvons construire une fonction qui va calculer ces features pour chaque audio et les enregistrer dans un dataframe.
Cette étape prend un peu de temps, en particulier le chargement des 1000 fichiers audio sur Python risque de durer de longues minutes. Pour vous éviter ça j’ai créée un fichier csv avec toutes les features, vous pouvez l’importer directement via mon drive.
Si vous tenez à le faire vous même, suivez cette partie.
Dans la cellule ci-dessous, on commence par créer un dictionnaire dans lequel nous importons tous les fichiers audio. Les clés du dictionnaire correspondent aux 10 genres différents.
# Définissons la liste avec les genres :
genres = ['blues', 'classical', 'country', 'disco', 'hiphop',
'jazz', 'metal', 'pop', 'reggae', 'rock']
# Création d'un dictionnaire avec les genres vide :
audio_files = {}
for g in genres:
audio_files[g] = []
# Remplissage du dictionnaire en important les fichiers audio avec Librosa :
for g in genres:
for audio in os.listdir(f'./genres/{g}'):
audio_files[g].append(librosa.load(f'./genres/{g}/{audio}')[0])Maintenant, pour remplir le dataframe nous allons devoir itérer sur ces audios et calculer les différentes features pour chacun des audios.
def audio_pipeline(audio):
features = []
# Calcul du ZCR
zcr = librosa.zero_crossings(audio)
features.append(sum(zcr))
# Calcul de la moyenne du Spectral centroid
spectral_centroids = librosa.feature.spectral_centroid(audio)[0]
features.append(np.mean(spectral_centroids))
# Calcul du spectral rolloff point
rolloff = librosa.feature.spectral_rolloff(audio)
features.append(np.mean(rolloff))
# Calcul des moyennes des MFCC
mfcc = librosa.feature.mfcc(audio)
for x in mfcc:
features.append(np.mean(x))
return featuresOn créé le dataframe :
# Définissons les noms des colonnes
column_names = ['zcr', 'spectral_c', 'rolloff', 'mfcc1', 'mfcc2', 'mfcc3',
'mfcc4', 'mfcc5', 'mfcc6', 'mfcc7', 'mfcc8', 'mfcc9',
'mfcc10', 'mfcc11', 'mfcc12', 'mfcc13', 'mfcc14', 'mfcc15',
'mfcc16', 'mfcc17', 'mfcc18', 'mfcc19', 'mfcc20', 'label']
# Création d'un dataframe vide
df = pd.DataFrame(columns = column_names)
# On itère sur les audios pour remplir le dataframe
i = 0
for g in genres:
for music in audio_files[g]:
df.loc[i] = audio_pipeline(music)+[g]
i+=1Je vous conseille d’exporter le dataframe au format csv pour ne pas avoir à télécharger et importer le fichier tar.gz à chaque fois :
df.to_csv('/content/music.csv', index = False)Evaluation de la qualité des données
A ce stade, que vous ayez suivi la partie précédente ou non vous devriez avoir un fichier csv avec toutes les features définies plus haut, pour toutes les musiques.
Importez ce fichier avec Pandas :
df = pd.read_csv("music.csv")Affichez les premières lignes du tableau pour voir à quoi il ressemble :
df.head()
Comme pour chaque projet en data science, on va faire l’étape de features selection. Il s’agit de faire une première étude préliminaire pour évaluer la qualité de nos données.
Il est d’usage de calculer les variances, les corrélations et regarder la répartition des classes. Le calcul des variances permet d’éliminer les features qui n’évoluent pas d’un son à l’autre et qui donc ne contiennent pas assez d’informations.
Les calculs de corrélations sont faits pour simplifier le dataset. Les implémentations des modèles classiques prennent souvent en compte les corrélations entres variables elles n’impacteront donc pas l’entraînement. Néanmoins, surtout lorsque l’on a beaucoup de features (de l’ordre du millier ou beaucoup plus suivant les applications), il peut être intéressant de retirer des variables qui sont corrélées pour réduire leur nombre.
Le calcul le plus critique, celui que vous ne devez pas laisser au hasard, est celui de la répartition des classes. Si les classes sont trop déséquilibrées, vous aurez des modèles biaisés en faveur des classes majoritaires, vous devrez donc affecter des poids à chaque classe en fonction de sa représentation. Evidemment, dans notre cas la base est parfaitement équilibrée, mais je vais quand même vous montrer le calcul a effectuer pour d’autres applications.
Variances
Pour le calcul de variances, vous devez fixer un seuil en dessous du quel vous éliminez la variable. Ce seuil est fixé de manière arbitraire et dépend de de vos variables.
selector = VarianceThreshold(threshold=(0.2))
selected_features = selector.fit_transform(df[['zcr', 'spectral_c', 'rolloff',
'mfcc1', 'mfcc2', 'mfcc3',
'mfcc4','mfcc5', 'mfcc6',
'mfcc7', 'mfcc8', 'mfcc9',
'mfcc10','mfcc11', 'mfcc12',
'mfcc13', 'mfcc14', 'mfcc15',
'mfcc16', 'mfcc17', 'mfcc18',
'mfcc19', 'mfcc20']])
pd.DataFrame(selected_features)Dans notre cas nous avons sélectionnés nos features une par une on les garde toutes.
Corrélations
Pour les corrélations on peut construire une matrice pour visualiser les corrélations plus facilement :
f = plt.figure(figsize=(12, 12))
plt.matshow(df.corr(), fignum=f.number)
plt.xticks(range(df.shape[1]), df.columns, fontsize=14, rotation=45)
plt.yticks(range(df.shape[1]), df.columns, fontsize=14)
cb = plt.colorbar()
cb.ax.tick_params(labelsize=14)
plt.title('Matrice de corrélation', fontsize=16, y=-0.15)Je ne détaillerais pas cette cellule, ce n’est qu’une question de visualisation. Retenez que df.corr() permet de calculer les corrélations une à une de vos variables.
Voici le résultat que l’on obtient :
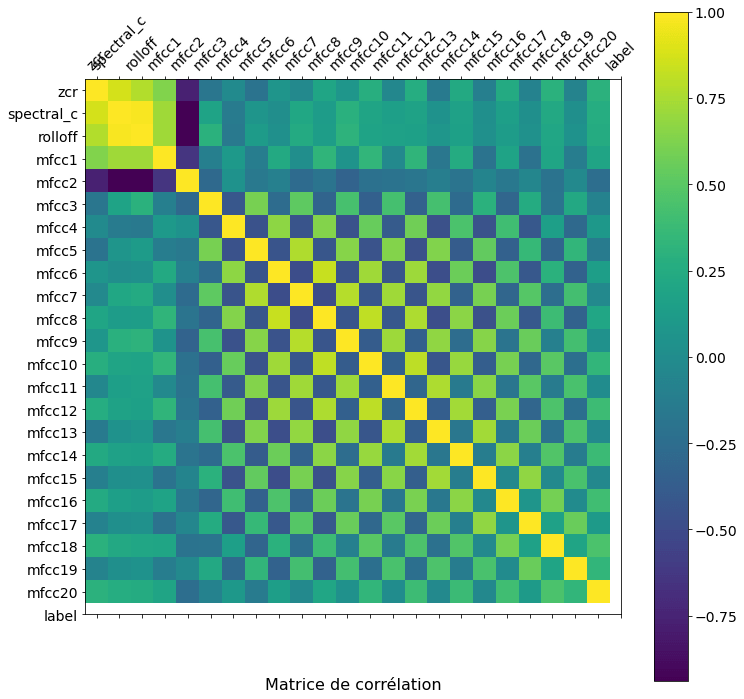
La lecture de cette matrice est très simple. Plus la couleur est proche du jaune plus les variables sont corrélées positivement. Vous voyez d’ailleurs que sur la diagonale on a que du jaune, ce qui est logique. Et plus la couleur se rapproche du bleu et plus les variables sont corrélées négativement.
Il est assez visible que plusieurs variables sont fortement corrélées. Un autre point remarquable est que les coefficients mfcc pairs (respectivement impairs) semblent être corrélés entre eux.
Répartitions des classes
Concernant la répartition des classes on peut afficher un donut pour la visualiser. Si vous avez déjà suivi d’autres tutoriels vous savez que j’aime les donuts hahaa !
Dans notre cas la base d’entraînement est parfaitement équilibrées puisqu’on a 100 musiques pour chaque genre représenté.
y = df['label']
values = np.unique(y,return_counts=True)[1]
labels = genres
sizes = values
# Choix des couleurs
colors =['#fff100','#ff8c00','#e81123','#ec008c','#0044bf','#0584f2','#0aaff1','#edf259','#a79674']
# Construction du diagramme et affichage des labels et des #fréquences en pourcentage
fig1, ax1 = plt.subplots()
ax1.pie(sizes, colors = colors, labels=labels, autopct='%1.1f%%', startangle=90)
# Tracé du cercle au milieu
centre_circle = plt.Circle((0,0),0.70,fc='white')
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Affichage du diagramme
ax1.axis('equal')
plt.tight_layout()
plt.show()On obtient la représentation suivante :
Constructions des différents modèles
Maintenant que la première partie est finie, entrons dans le vif du sujet. Dans cette partie nous allons construire des modèles de classification et allons les comparer pour voir lequel convient le mieux.
Voici les différentes méthodes que nous essayerons, je ne vais pas expliquer les détails de chaque algorithme, ils ont déjà été abordés dans d’autres articles (je vous mets les liens!) :
Pour pallier les particularités de l’implémentations de chaque modèle, nous construirons les ensembles d’entraînement à chaque fois.
Support Vector Machines
De manière générale les SVM sont très fiables lorsqu’ils sont appliqués à des problèmes de classification binaire. Leur généralisation pour des problèmes de plus grandes dimensions se font à travers des méthodes comme One vs All, ce qui engendre souvent une perte de performances.
Constructions des ensembles d’entraînement
On construits notre X et notre y puis on les split pour l’entraînement :
X = df[['zcr', 'spectral_c', 'rolloff', 'mfcc1', 'mfcc2', 'mfcc3',
'mfcc4', 'mfcc5', 'mfcc6', 'mfcc7', 'mfcc8', 'mfcc9',
'mfcc10', 'mfcc11', 'mfcc12', 'mfcc13', 'mfcc14', 'mfcc15',
'mfcc16', 'mfcc17', 'mfcc18', 'mfcc19', 'mfcc20']]
y = df['label']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)Entraînement du modèle
L’implémentation du SVM se fait facilement avec scikit-learn. On ne s’intéresse pas à l’optimisation des paramètres puisqu’on peut déjà prédire que SVM ne donnera pas satisfaction (on fait ça pour le fun haha!).
On implémente aussi une cross validation pour mieux évaluer notre modèle.
model_svm = SVC()
model_svm.fit(X_train, y_train)
print('Train score : ', model_svm.score(X_train,y_train))
print('Test score : ', model_svm.score(X_test,y_test))
k_3 = np.arange(1,31)
tr_score_3, val_score_3 = validation_curve(model_svm, X_train, y_train, 'C', k_3, cv = 5)
#5 splits sets de cross validation, on fait la moyenne des scores obtenus sur chacun des 5 splits
train = model_svm.predict(X_train)
predictions = model_svm.predict(X_test)
plt.plot(k_3, val_score_3.mean(axis = 1), label = 'validation')
plt.plot(k_3, tr_score_3.mean(axis = 1), label = 'train')
plt.ylabel('score')
plt.xlabel('C')
plt.legend()Voici le résultat obtenu :
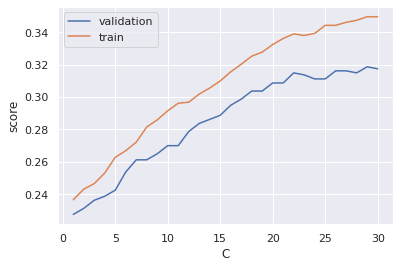
Il est clair que l’on peut faire beaucoup mieux !
Mesures des performances
On peut tracer une matrice de confusion qui nous permettra de visualiser pour quelles classes le modèle est performants et pour quelles classes ne l’est pas.
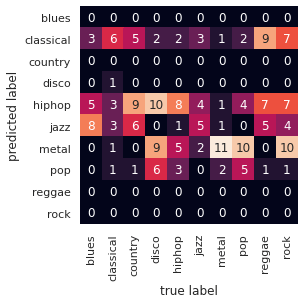
Inutile de préciser qu’on à un gros problème avec ce modèle !
5 genres différents sont ignorés par le modèle. Et ceux qui sont pris en compte ne sont pas bien classés. En particulier le modèle confond entre l’hiphop et la disco ou entre le metal et le rock. On peut faire beaucoup mieux !
k-nn : k nearest neighbours
On commence par reconstruire nos ensembles d’entraînement. SVM et k-nn prennent les mêmes ensembles en entrée :
X = df[['zcr', 'spectral_c', 'rolloff', 'mfcc1', 'mfcc2', 'mfcc3',
'mfcc4', 'mfcc5', 'mfcc6', 'mfcc7', 'mfcc8', 'mfcc9',
'mfcc10', 'mfcc11', 'mfcc12', 'mfcc13', 'mfcc14', 'mfcc15',
'mfcc16', 'mfcc17', 'mfcc18', 'mfcc19', 'mfcc20']]
y = df['label']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)Entraînement du modèle
On peut s’atteler à l’entraînement du modèle. On choisit d’abord un nombre de voisins arbitraire de 5 :
model_1 = KNeighborsClassifier(n_neighbors = 5)
model_1.fit(X_train, y_train)
print('Train score :', model_1.score(X_train,y_train))
print('Test score :', model_1.score(X_test,y_test))Voici le résultat qu’on obtient :
Train score : 0.49375
Test score : 0.29C’est toujours très faible comme performances.
On peut essayer d’optimiser le nombre de voisins en utilisant une validation croisée encore une fois :
k_1 = np.arange(1, 31)
train_score_1, val_score_1 = validation_curve(model_1, X_train, y_train, 'n_neighbors', k_1, cv = 5)
#5 splits sets de cross validation, puis on fait la moyenne des scores obtenus sur chacun des 5 splits
plt.plot(k_1, val_score_1.mean(axis = 1), label = 'validation')
plt.plot(k_1, train_score_1.mean(axis = 1), label = 'train')
plt.ylabel('score')
plt.xlabel('n_neighbors')
plt.legend()On trace les courbes d’évolution des performances en fonction de la valeur de k :
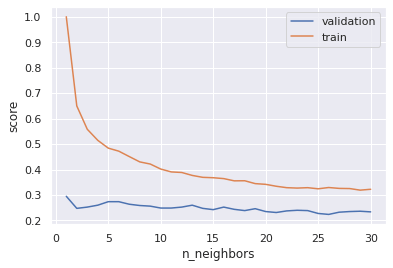
On voit que quelque soit la valeur de k le modèle ne donne pas de bons résultats.
Par ailleurs, il est intéressant de remarquer que plus le nombre de voisins est faible, plus le risque d’overfitting est élevé. Rien de surprenant, c’est évidemment un résultat que l’on aurait pu prédire.
Mesures des performances
Comme pour SVM on trace la matrice de confusion :
np.max(val_score_1.mean(axis = 1))
np.argmax(val_score_1.mean(axis = 1)) + 1
#+1 pour avoir le nombre de voisins optimal (indice commençant à 0)
#on trouve entre 5 et 10 voisins pour environ 30-35% de réussite
sns.set()
mat = confusion_matrix(y_test, model_1.predict(X_test))
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, xticklabels=genres, yticklabels=genres)
plt.xlabel('true label')
plt.ylabel('predicted label')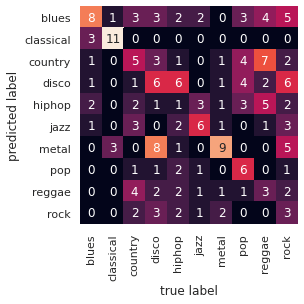
Les résultats sont déjà un peu meilleurs qu’avec SVM, notamment pour certaines classes comme la musique classique, la disco et le metal. Cela peut s’expliquer par le fait que ce sont des styles musicaux plus facilement détectables.
Néanmoins, nous ne pouvons clairement pas nous satisfaire de tels résultats. Par exemple on observe dans cette matrice des confusions étranges comme disco/rock ou encore country/rock.
On a encore un peu de travail à faire, mais ça va bientôt marcher, restez concentrés !
Random forest
SVM et k-nn ne sont pas très adaptés à ce genre de données, c’est ce qui explique les performances médiocres que l’on obtient.
Pour des dataset comme celui que l’on a construits, il est préférable d’utiliser des méthodes qui reposent sur des arbres de décisions. Random forest ou XGBoost sont de très bons choix !
Constructions des ensembles d’entraînement
Avant tout, on prépare les données en distinguant l’échantillon d’entrainement de l’échantillon de test.
features = df
# valeurs à prédire
labels = np.array(features['label'])
# supprime les labels des données
features = features.drop('label', axis = 1)
# sauvegarde le nom de features
feature_list = list(features.columns)
# conversion en numpy array
features = np.array(features)
# séparer les données en training and testing sets
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size = 0.25, random_state = 0)
print('Training Features Shape:', train_features.shape)
print('Training Labels Shape:', train_labels.shape)
print('Testing Features Shape:', test_features.shape)
print('Testing Labels Shape:', test_labels.shape)
sc = StandardScaler()
train_features = sc.fit_transform(train_features)
test_features = sc.transform(test_features)On a maintenant des données prêtent à l’emploi pour entraîner un modèle random forest.
Optimisation des hyper-paramètres
Random forest est un modèle très flexible qui peut s’adapter à de nombreuses situations. L’inconvénient est qu’on ne peut pas le paramétrer facilement, on doit employer des techniques d’optimisation.
On affiche dans un premier temps tous les hyper-paramètres avec lesquelles il est possible de jouer.
rf = RandomForestClassifier(random_state = 0)
from pprint import pprint
print('Parameters currently in use:\n')
pprint(rf.get_params())Parameters currently in use:
{'bootstrap': True,
'ccp_alpha': 0.0,
'class_weight': None,
'criterion': 'gini',
'max_depth': None,
'max_features': 'auto',
'max_leaf_nodes': None,
'max_samples': None,
'min_impurity_decrease': 0.0,
'min_impurity_split': None,
'min_samples_leaf': 1,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0.0,
'n_estimators': 100,
'n_jobs': None,
'oob_score': False,
'random_state': 0,
'verbose': 0,
'warm_start': False}Ca fait beaucoup trop d’hyperparamètres, on ne pourra clairement pas tous les optimiser ! On décide de se focaliser sur le nombre d’arbres, la profondeur des arbres et le nombre d’échantillon minimal requis par nœuds et par feuilles.
Un random search permet de se faire une première idée des valeurs optimales des différents hyper-paramètres, en balayant de façon très large les différentes possibilités et en selectionnant les meilleures combinaison par validation croisée.
On affiche la grille à tester.
# nombre d'arbres
n_estimators = [500, 1000, 2000, 3000, 4000, 5000]
# profondeur max de l'arbre
max_depth = [20]
max_depth.append(None)
# nombre d'échantillon min nécessaire par noeuds
min_samples_split = [2, 4]#[2]
# nombre d'échantillon min nécessaire par feuilles
min_samples_leaf = [1, 2]#[1]
# création de la grille
random_grid = {'n_estimators': n_estimators,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
}
pprint(random_grid){'max_depth': [20, None],
'min_samples_leaf': [1, 2],
'min_samples_split': [2, 4],
'n_estimators': [500, 1000, 2000, 3000, 4000, 5000]}Pour des questions de temps d’exécution et compte tenu de la taille de la base de données, on lance ici un random search à 3 blocs réduit à 10 combinaisons.
# création du modèle
rf = RandomForestClassifier(random_state = 0, max_features = 'sqrt', bootstrap = True)
# random search
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 10, cv = 3, verbose=2, random_state=0, n_jobs = -1)
# fit le modèle
rf_random.fit(train_features, train_labels)
pd_res = pd.concat([pd.DataFrame(rf_random.cv_results_["params"]),pd.DataFrame(rf_random.cv_results_["mean_test_score"], columns=["Accuracy"])],axis=1)
pd_res = pd_res.sort_values('Accuracy', ascending=False)
print(rf_random.best_params_)
pd_res.head(5)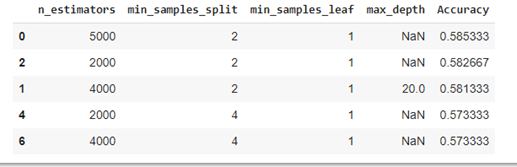
On peut déjà se réjouir que l’on ait des résultats beaucoup plus intéressants qu’avec SVM et k-nn.
On retient la combinaison gagnante de 4000 arbres, à laquelle on ajoute la troisième. En revanche, utiliser plus de 4000 arbres semble contre-productif puisque des 5000 arbres, on observe une baisse de performance.
Le nombre d’échantillon minimal requis par nœuds et par feuilles ayant été déterminé par random search, on approfondit nos recherches sur le nombre et la profondeur des arbres par l’intermédiaire d’un grid search (qui est une autre méthode d’optimisation).
Voici les paramètres à optimiser :
param_grid = {
'max_depth': [20, None],
'min_samples_split': [2],
'n_estimators': [2000, 4000]
}
pprint(param_grid)On lance grid search :
# création du modèle
rf = RandomForestClassifier(random_state = 0, bootstrap=True)
# grid search
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid, cv = 3, n_jobs = -1, verbose = 2)
grid_search.fit(train_features, train_labels)
pd_res = pd.concat([pd.DataFrame(grid_search.cv_results_["params"]),pd.DataFrame(grid_search.cv_results_["mean_test_score"], columns=["Accuracy"])],axis=1)
pd_res = pd_res.sort_values('Accuracy', ascending=False)
pd_res.head(5)Voici les résultats que l’on obtient :
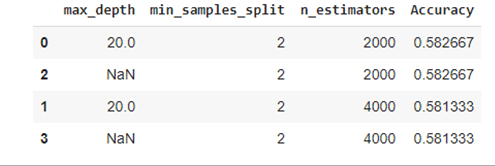
La meilleure option ici semble être de choisir 4000 arbres d’une profondeur maximale de 20 niveaux.
Attention à ne pas prendre une profondeur maximale trop grande. C’est la source première d’overfitting avec random forest.
Entraînement du modèle
On entraîne maintenant notre modèle avec les valeurs d’hyperparamètres que l’on a trouvé.
# création du modèle
rf = RandomForestClassifier(n_estimators=4000, max_features='sqrt', max_depth=20, min_samples_split=2, min_samples_leaf=1, bootstrap=True, criterion='gini' ,random_state=0)
# fit le modèle
rf.fit(train_features, train_labels)
# prédictions
predictions = rf.predict(test_features)
# Zero_one_loss error
errors = zero_one_loss(test_labels, predictions, normalize=False)
print('zero_one_loss error :', errors)
# Accuracy Score
accuracy_test = accuracy_score(test_labels, predictions)
print('accuracy_score on test dataset :', accuracy_test)
print(classification_report(predictions, test_labels))Le modèle se trompe 102 fois sur 230, pour une précision de 59.2%. Ces performances sont bien meilleures que les précédents modèles!
La country, le disco, le hiphop, le jazz et le rock sont assez mal reconnus. On pourrait l’expliquer par le fait que ces genres utilisent généralement des instruments aux sonorités assez similaires (hiphop, jazz et rock par exemple), que les features ne sont pas assez pertinents ou que notre modèle est mauvais.
A l’inverse, la pop ainsi que le classique sont très bien traités, renforçant l’idée que certains genres sont par nature plus facilement distinguable que d’autres.
Mesures des performances
Lorsqu’il est question de classifications le choix des métriques utilisées pour évaluer un modèle est primordial. Voici quelques unes des métriques que l’on pourrait considérer :
- Précision : c’est la métrique la plus simple que l’on ait, il s’agit simplement de la proportion de prédictions correctes parmi toutes les prédictions faites par le modèle.
- Recall : le recall est initialement une métrique utilisée pour des classifications binaires correspond à la proportion de prédictions positive lorsqu’on s’attend à ce que le résultat soit positif.
- F1-Score : le F1-Score est une combinaison des deux métriques précédente, il est souvent utilisé dans les papiers de recherches pour comparer les performances entre deux classifieurs.
Bien que le F1-Score et le Recall soient initialement des métriques prévues pour des classifieurs binaires, il est très facile de les adapter à des situations multi-classes.
Pour pouvoir visualiser les performances et quand la taille de vos données vous le permet, le meilleure option reste la matrice de confusion. Elle vous donnera à la fois une mesure des performances macroscopique mais aussi elle vous permettra de comprendre ce qui se passe à l’échelle de chaque classes.
sns.set()
mat = confusion_matrix(test_labels, predictions)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, xticklabels=genres, yticklabels=genres)
plt.xlabel('true label')
plt.ylabel('predicted label')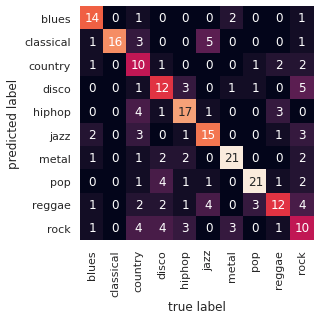
Les résultats sont déjà plutôt satisfaisants.
Interprétation des résultats
Un des avantages de random forest par rapport à d’autres modèles de machine learning, est qu’il permet d’interpréter facilement les résultats que l’on obtient.
A l’heure ou l’explicabilité des modèles devient un sujet primordial, les arbres de décisions ont un gros avantage sur les autres modèles !
On peut par exemple afficher un diagramme représentant l’importance des features dans le choix de classification :
plt.style.use('fivethirtyeight')
importances = list(rf.feature_importances_)
x_values = list(range(len(importances)))
plt.bar(x_values, importances, orientation = 'vertical')
plt.xticks(x_values, feature_list, rotation='vertical')
plt.ylabel('Importance'); plt.xlabel('Variable'); plt.title('Variable Importances')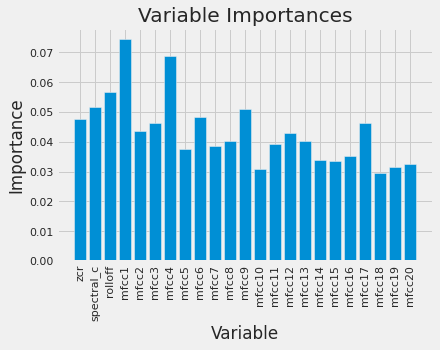
On voit par exemple que mfcc1 est la feature la plus importante. Il est clair que les features ont à peu près la même importance, ce qui nous rassure sur la sélection faite au début.
Ici l’interprétation ne nous permet pas de tirer de conclusions, mais dans certains cas elle peut être utile. Par exemple, si vous souhaitez prédire les chances d’embauche d’une personne dans une entreprise et que vous voyez que la variable âge à une trop grande importance, c’est peut être que votre modèle est biaisé.
XGBoost
XGBoost est assez similaire à random forest dans le principe, on devrait avoir des performances très proches. Je vais supposer que l’optimisation des paramètres a déjà été faite (le principe est le même que précédemment, et les codes sont sur colab).
Entraînement du modèle
On peut entraîner le modèle avec les paramètres sélectionnés dans l’étape d’optimisation :
#model = XGBClassifier(objective='multi:softprob', colsample_bylevel=1, colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=3, max_depth=10, min_child_weight=1, n_estimators=300, subsample=0.8, random_state = 0)
model = XGBClassifier(objective='multi:softprob', colsample_bylevel=1, colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0, max_depth=10, min_child_weight=1, n_estimators=300, subsample=0.8, random_state = 0)
# fit the model with the training data
model.fit(train_features, train_labels)
# predict the target on the test dataset
predict_test = model.predict(test_features)
# Accuracy Score on test dataset
accuracy_test = accuracy_score(test_labels, predict_test)
print('\naccuracy_score on test dataset : ', accuracy_test)Mesures des performances
On obtient un score de 57.6%
Le score est en dessous du random forest. Ce résultat surprenant pourrait s’expliquer par le fait qu’avec les données disponibles (nombres, features, …), il ne soit pas possible de faire mieux.
Néanmoins, nous avons encore un modèle à tester, voyons ce que l’on peut faire !
Réseau de neurones convolutionnel (CNN) sur les spectrogrammes des musiques
Dans un article de Towards data science sur ce problème une approche assez inhabituelle a été suggérée par l’auteur, nous avons décidé de l’implémenter pour vérifier si cela peut fonctionner.
L’idée est d’entraîner le modèle de classification non pas sur les features que nous avons sélectionnées mais sur les images représentants les spectres des musiques. Pour cela nous allons d’abord construire un pipeline pour récupérer les spectres audio et encoder les images crées. Nous ferons la classification des images avec des réseaux de convolutions.
L’utilisation de réseaux de neurones convolutionnels représente la meilleure approche lorsqu’il s’agit de faire de la classification d’images.
Création des images
Dans la cellule ci-dessous, nous associons tous les fichiers audio à leur spectrogramme. Pour cela nous devons itérer sur ces fichiers, ploter leurs spectrogrammes respectifs et sauvegarder l’image dans un dossier que nous avons créé au préalable.
Tous les spectrogrammes seront ensuite accessibles depuis le dictionnaire audio_files :
genres = ['blues', 'classical', 'country', 'disco', 'hiphop',
'jazz', 'metal', 'pop', 'reggae', 'rock']
audio_files = {}
for g in genres:
audio_files[g] = []for g in genres:
for audio in os.listdir(f'./genres/{g}'):
audio_files[g].append(librosa.core.load(f'./genres/{g}/{audio}'))Voici un extrait des images à partir des quelles nous allons construire notre modèle :

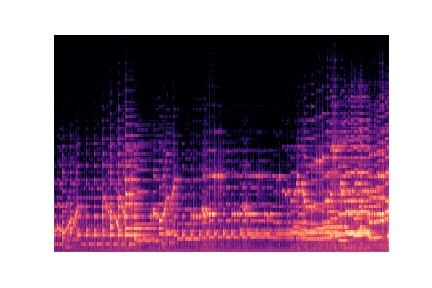
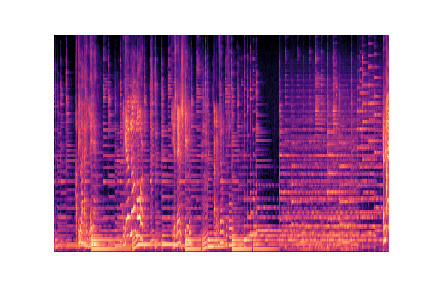
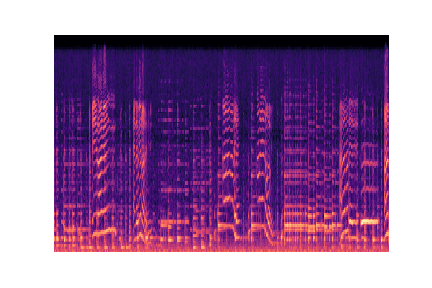
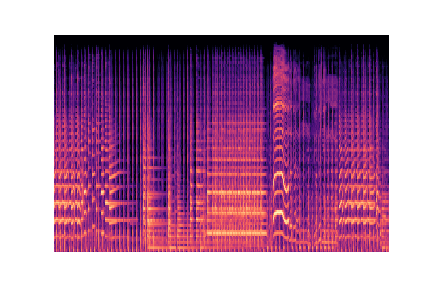
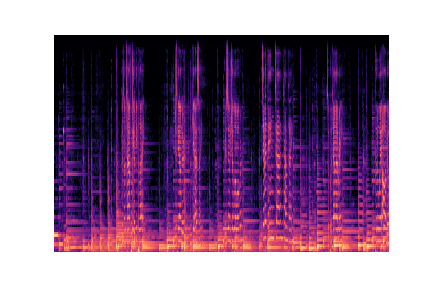
Preprocessing
On peut maintenant stocker toutes les images sous forme de matrices numpy dans un vecteur X :
Nous allons maintenant mettre en ordre nos données d’entraînement. On doit avoir un array que nous appellerons X (pour ne pas confondre avec le précédent X) constitué de toutes les matrices des images, ainsi qu’un array appelé y_cnn avec tous les labels.
mel_specs = []
for g in genres:
for audio in audio_files[g]:
y = audio[0]
sr = audio[1]
spect = librosa.feature.melspectrogram(y=y, sr=sr, n_fft=2048, hop_length=1024)
spect = librosa.power_to_db(spect, ref=np.max)
# On modifie la taille des images 128 x 660 en gardant les paramètres proposés dans l'article initial
if spect.shape[1] != 660:
spect.resize(128,660, refcheck=False)
mel_specs.append(spect)
X = np.array(mel_specs)On peut maintenant créer le vecteur des labels y_cnn, pour l’instant nos images sont dans l’ordre la construction de y_cnn est triviale :
y_cnn = []
for i in range(len(genres)):
y_cnn += 100*[i] # On a 100 images pour chaque genre
y_cnn = np.array(y_cnn)Pour pouvoir utiliser y_cnn il faut la transformer en variables catégoriques par un encodage One-Hot, scikit-learn permet de le faire très facilement.
On split ensuite nos données en données de test et données d’entraînements :
y_cnn = to_categorical(y_cnn)
x_cnn_train, x_cnn_test, y_cnn_train, y_cnn_test = train_test_split(X, y_cnn)On pense à normaliser les données, c’est important pour l’analyse d’images :
x_cnn_train /= np.min(x_cnn_train)
x_cnn_test /= np.min(x_cnn_train)A présent on met en forme nos données pour l’entraînement :
x_cnn_train = x_cnn_train.reshape(x_cnn_train.shape[0], 128, 660, 1)
x_cnn_test = x_cnn_test.reshape(x_cnn_test.shape[0], 128, 660, 1)A ce stade nous avons bien deux arrays X et y_cnn. X contient toutes les matrices représentants les images des spectrogrammes et y_cnn contient les labels pour chaque image.
Vérifions les tailles de x_cnn et y_cnn pour être sur qu’il n’y a pas de problème :
print(x_cnn_train.shape)
print(y_cnn_train.shape)Conception de l’architecture du réseau et entraînement
On commence par construire notre réseau de neurones :
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=(128,660,1)))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Conv2D(64,
kernel_size=(3, 3),
activation='relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Dropout(0.3))
model.add(tf.keras.layers.Conv2D(32,
kernel_size=(3, 3),
activation='relu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dropout(0.3))
model.add(tf.keras.layers.Dense(64, activation='relu'))
model.add(tf.keras.layers.Dense(32, activation='relu'))
model.add(tf.keras.layers.Dense(10, activation='softmax'))Avant de lancer l’entraînement du réseau, voyons un résumé des couches que l’on a :
model.summary()
On compile le modèle en selectionnant la categorical crossentropy comme perte avec l’optimiseur ADAM.
model.compile(
loss="categorical_crossentropy",
optimizer="adam",
metrics=["accuracy"]
)On peut maintenant commencer l’entraînement :
history = model.fit(x_cnn_train,
y_cnn_train,
epochs=25,
validation_data = (x_cnn_test,y_cnn_test))Regardons l’évolution de l’accuracy et de la loss au fil des époque :
loss_curve = history.history["loss"]
acc_curve = history.history["accuracy"]
loss_val_curve = history.history["val_loss"]
acc_val_curve = history.history["val_accuracy"]
plt.plot(loss_curve, label="Train")
plt.plot(loss_val_curve, label="Val")
plt.legend(loc='upper left')
plt.title("Loss")
plt.show()
plt.plot(acc_curve, label="Train")
plt.plot(acc_val_curve, label="Val")
plt.legend(loc='upper left')
plt.title("Accuracy")
plt.show()On obtient les résultats suivants :
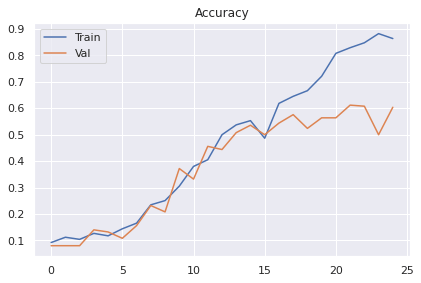
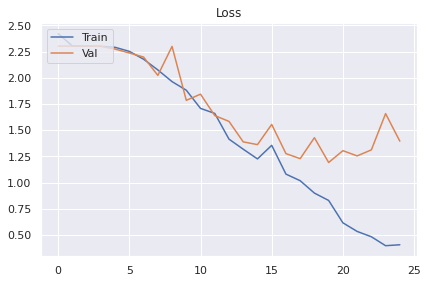
On voit vraiment que l’on atteint un plateau autour de 60% et qu’il sera difficile de faire plus. Au delà d’une trentaine d’époques le modèle overfit.
Mesures des performances
On finit avec un score de performance de 60.4%. J’étais assez sceptique concernant cette méthode mais finalement elle donne des résultats pas si mauvais.
Traçons la matrice de confusion :
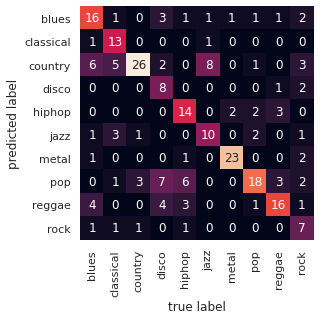
On voit qu’avec cette approche les performances sont encore meilleurs. On a le sentiment qu’en optimisant encore notre CNN on pourrait grapiller encore quelques points.
C’est un résultat qui nous a surpris au départ mais qui finalement semble assez logique. Le spectrogramme d’un son caractérise ce son et contiendra toujours plus d’informations que celles que l’on peut extraire manuellement.
Un des inconvénients de l’utilisation des CNN est le manque d’interprétabilité. On n’a pas de moyens simples d’identifier les caractéristiques qui permettent de discrimer des sons, alors qu’avec random forest par exemple, on pouvait classer les features par ordre d’importance. C’est le fameux dilemme explicabilité/performances.
Conclusion et analyse critique des résultats
Les premiers résultats que l’on obtient sont plutôt intéressants même si on pouvait espérer obtenir de meilleurs performances.
- SVM : 17.5
- k-nn : 29%
- RF : 59.2%
- XGB : 57.6%
- CNN : 60.4%
Il y a certains points que l’on pourrait améliorer et qui peuvent peut-être expliquer ces performances :
- Le choix des features est important mais il est aussi très subjectif. En pratique le choix des features doit se faire par des gens qui connaissent bien l’analyse musicale.
- La classification de musiques par genre est une tâche qui est parfois difficile même pour un être humain. D’ailleurs il n’est pas rare d’observer des débats concernant le genre à laquelle une musique appartient.
- Nous n’avions que 100 exemples de musiques par classe à disposition. C’est suffisant mais pour ce genre de tâches plus la base d’apprentissage est grande plus les performances sont bonnes.
- Dans le cas du réseau convolutionnel sur les spectrogrammes, nous avons eu des difficultés pour éviter le surapprentissage. L’ajout de dropout n’a pas permis de résoudre le problème. Une option que l’on aurait pu experimenter est d’utiliser la data augmentation. Rajouter des pistes audio en modifiant légérement le signal par exemple en ajoutant du bruit. C’est une technique qui fonctionne surtout pour l’analyse d’images mais elle pourrait donner de bons résultats dans notre cas.
Bibliographie
- Music Genre Classification with Python, Towards data science, Parul Pandey : https://towardsdatascience.com/music-genre-classification-with-python-c714d032f0d8
- Zero Crossing Rate, Wikipédia : https://fr.wikipedia.org/wiki/Zero_Crossing_Rate
- Cepstre, Wikipédia : https://fr.wikipedia.org/wiki/Cepstre
- Spectral Rolloff point, Mathworks : https://www.mathworks.com/help/audio/ref/spectralrolloffpoint.html
- Music genre classification with CNN, Towards data science, Lelan Roberts : https://towardsdatascience.com/musical-genre-classification-with-convolutional-neural-networks-ff04f9601a74
- Construction and evaluation of a robust multifeature speech/music discriminator, Eric Scheirer & Malcolm Slaneyy : https://www.ee.columbia.edu/~dpwe/papers/ScheiS97-mussp.pdf



Leave a Comment